Interaction of Electromagnetic Radiation: Quantum Structures
| ✅ Paper Type: Free Essay | ✅ Subject: Physics |
| ✅ Wordcount: 1801 words | ✅ Published: 09 Mar 2018 |
Preparation and Characterisation of Quantum Dot Infrared Photo Detector and Its Application in Night Vision Devices
Submitted by
Mangala Gowri M
Focus of the study during this period was to understand interaction of electromagnetic radiation with quantum structures.
Interband transition and intraband transition are two types of transition possible in semiconductors. Intraband transitions are unique for the quantum semiconductor structures. Intraband transitions between the quantized energy levels are possible depending on several parameters. The resonance wavelength depends on effective masses of the carriers, parameters like size, shape and composition of the quantum structures.
Practical observations made on quantum structures like quantum wells and quantum dots were very interesting. “The first direct observation of infrared absorption between conduction subbands of n-doped GaAs/AlGaAs quantum wells was reported in 1985. It was confirmed that intersubband transitions between electronic states of quantum wells are strongly polarized along the confinement potential direction.” [1] Therefore light whose polarization has component along the confinement potential direction gets absorbed. Therefore “light must have a polarization component perpendicular to the quantum well layers.” [1] This is the strong limitation for the quantum well infrared photo detectors. On the other hand, quantum wires and quantum dots theoretically do not have this limitation on the polarization direction of incident radiation. For quantum well polarization, direction radiation should not be normal (perpendicular) to the confinement potential direction, whereas this type of normal incidence is allowed for quantum dots.
Oscillator Strength:
“Oscillator strength is a dimensionless quantity that expresses the probability of absorption or emission of radiation in transitions between energy levels of an atom or molecule.” [2] When an electronic transition occurs an oscillating dipole moment will be induced by interaction of electric field of the system with electromagnetic radiation. The following illustration explains the mechanism of transition in a system in general. Suppose an electron changes its energy from En to Em by changing its state from ψn to ψm. During the transition it will be in a state which is superposition of the two states.
Ψ = aψn + bψm
Probability that the electron in the state ψn is |a|2 and probability that it is in state ψm is |b|2 so that at any time |a|2 + |b|2 =1. We can see that expectation value  , γnm is the transition frequency.
, γnm is the transition frequency.
Transition Dipole Moment:
Transition dipole moment is the dipole moment associated with the transition between two states. It is a complex vector quantity. It encodes phase factors associated with the two states. The direction of this dipole moment is the polarization of the transition. The polarization of the transition determines the interaction of the system with electromagnetic radiation with a given polarization. Square of the dipole moment of transition gives the strength of the transition.
Transition dipole moment is off-diagonal matrix element of position operator multiplied by the particle’s charge. Classically, dipole moment is product of charge and separation between the two charges. In the presence of an electric field, the two charges will experience a force in opposite direction so that a torque acts on the dipole. Similarly, during transition, coupling between an electromagnetic wave and transition dipole moment of the system depends on the charge distribution within the system, strength of the field and the relative polarization of the field and the transition. Also transition dipole moment depends on the geometries and relative phases of the two states involved in transition. The concept of transition dipole moment is very useful to determine whether a transition is allowed or not. If the integral defining transition dipole moment is nonzero, that transition is allowed.
Perturbation Theory:
To understand the mechanism of interaction between the system and electromagnetic radiation, we adopt quantum mechanical perturbation theory. Incident radiation is treated as a perturbation. Electromagnetic radiation provides a time dependent potential, which assists quantum jumps between energy levels. So total Hamiltonian of the system has two parts, one is time independent and another is time dependent. If time dependent part is small compared to time independent part, then that can be treated as a perturbation.
Considering two level system, where Ψa and Ψb are two eigen states of unperturbed Hamiltonian H0. The two states are orthonormal. Any other state of the system can be written as a linear combination of those two states.
Ψ(0) = Ca Ψa + Cb Ψb
Ca and Cb are constants, which include information about probability of finding the system in respective states.
Suppose we are curious to know the state of the system after a time t. If there is time dependent perturbation, Ψ(t) is again superposition of the two states. Not only the two states evolve with time, but also coefficients Ca and Cb are also functions of time. If we can determine Ca(t) and Cb(t) we can understand the system at time t. Several mathematical steps lead us to
ÄŠa = 
And
ÄŠb = 
Where ÄŠa and ÄŠb are time derivatives of Ca(t) and Cb(t) respectively.
Both of the above equations taken together are equivalent to time dependent Schrodinger equation for a two level system.
The diagonal matrix elements of H’ vanish.
Therefore,
ÄŠa = 
ÄŠb = 
With 
Considering that H’ is small, above equations can be solved by a process called successive approximations. Here we also consider that perturbation is having sinusoidal time dependence.

Then 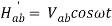
And 
In the first order we have

ω is the driving frequency and ω0 is the transition frequency.
If ω and ω0 are very close to each other second term in the square brackets dominates. So we can say ω + ω0 >> | ω0 – ω|
We drop first term and after simplification

The transition probability gives the probability that a particle started from the initial state will reach at final state in time t.


We can see here that transition probability as a function of time oscillates sinusoidally.

Fig: Transition probability as a function of time, for sinusoidal perturbation.
Maximum value of probability is 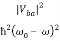 . The probability of rising to the maximum value is much less than 1 for small perturbation. Another thing to observe here that the probability of transition is highest when ω
. The probability of rising to the maximum value is much less than 1 for small perturbation. Another thing to observe here that the probability of transition is highest when ω  ω0.
ω0.

Fig: Transition probability as a function of driving frequency.
Thus as time goes on width of the peak becomes narrower and height of the peak becomes higher. That means that the system will undergo transition with higher probability.
Emission and Absorption of Radiation:
An electromagnetic wave consists of transverse oscillating electric and magnetic fields. An atom reacts primarily to the oscillating electric component of radiation. Assume that an atom is exposed to a sinusoidally oscillating electric field. Consider that the field is polarized along z direction.
Then the perturbing Hamiltonian is written as

Note: Considering that the period of oscillation of the field is long compared to the time taken by the charge to move around within the atom we adopt electrostatic formula for Vab that is equal to 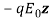
Then

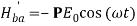
Where P =  is transition dipole moment.
is transition dipole moment.
Ψ is an odd or even function of z. We consider that the diagonal matrix elements of H’ vanish. Then the interaction of radiation with the system is governed by precisely the kind of oscillatory perturbation with Vab 
Note: P is off-diagonal matrix element of z component of dipole moment operator qr.
Transition probability is proportional to the energy density of the perturbing fields. And we see that the probability is proportional to time.

If incident radiation is monochromatic, transition probability oscillates. However, if the system is exposed to incoherent spread of frequencies that flopping nature disappears. The transition rate will be a constant.

In the calculations, we have assumed that the direction of propagation of perturbing radiation is y direction and it is polarized along z axis. However, in practice the system (like quantum well, quantum dot) is exposed to a radiation coming from all directions and with all possible polarizations. Then the energy of the field is shared equally among these different modes. So in the place of  we have to substitute the average of |P.n|2 with n is the direction of polarization of radiation. Average is over all polarizations and all incident directions.
we have to substitute the average of |P.n|2 with n is the direction of polarization of radiation. Average is over all polarizations and all incident directions.
Quantum Well:
A quantum well can be considered as idealized square, finite and symmetrical potential well. It is now evident that absorption of radiation by quantum well depends on the direction of the transition dipole moment and direction of polarization of incident radiation. It can be shown that the wave function of quantum well is a even function in ground state and it is alternatively even or odd in higher states.
In order to P be nonzero Ψa and Ψb should be of opposite parity since z is odd. In addition, direction of P depends on Ψa and Ψb. Since the wavefunction of the quantum well has only z component, transition dipole moment will also be directed along the z direction i.e. along the direction of potential Vwell(z).
In the case of normal incidence, the polarization of radiation is perpendicular to the walls of the well barrier or to the potential. The n that refers to polarization direction of radiation is in xy plane.
So choosing cylindrical polar coordinates, we have

And  . Thus,
. Thus,  .
.
Then, 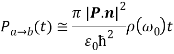

Which implies that normal incidence in quantum wells is forbidden.
The polarization selection rules for transitions in quantum wells are summarized below.
|
Polarization |
Ex |
Ey |
Ez |
|
Propagation along z |
Forbidden |
forbidden |
Impossible |
|
Propagation along x |
Impossible |
forbidden |
Allowed |
|
Propagation along y |
Forbidden |
impossible |
Allowed |
Quantum Dot:
Quantum dot is a quantum structure, which is confined three dimensionally. Thus, the confinement potential has all the three x, y, z components. Similarly the wave functions representing the states of quantum dot have x, y, z components. So the scalar product between transition dipole moment and the polarization direction of incident radiation will not be equal to zero.
Average of  is not zero in quantum dots. Thus, the quantity
is not zero in quantum dots. Thus, the quantity  in quantum dots is nonzero. There is no restriction for direction of polarization of radiation theoretically. Even though normal incidence intraband absorption is forbidden in quantum wells, they are allowed in quantum dots. This is major fact of great interest in the development of infrared photodetectors.
in quantum dots is nonzero. There is no restriction for direction of polarization of radiation theoretically. Even though normal incidence intraband absorption is forbidden in quantum wells, they are allowed in quantum dots. This is major fact of great interest in the development of infrared photodetectors.
I attended a two-day collaborator’s workshop organized by Centre of ART, SIT, Tumkur from 20-02-2014 to 21-02-2014.
Study Plan: In the next half year, focus of the study will be MOCVD growth process of quantum dots.
Signature of the CandidateSignature of the Guide
(Manala Gowri M) (Prof. (Dr.) Ganesh N. Raikar)
References:
- A. Weber. Intraband Spectroscopy of Semiconductor quantum dots, 1998.
2. http://en.wikipedia.org/wiki/Oscillator_strength
3. Proefschrift. Optical Properties of Semiconductor Quantum Dots, 2011
4. Griffith. D.J, Introduction to quantum Mechanics, 2nd Ed, Pearson Education Inc, 2006.
Cite This Work
To export a reference to this article please select a referencing stye below:
Related Services
View allDMCA / Removal Request
If you are the original writer of this essay and no longer wish to have your work published on UKEssays.com then please click the following link to email our support team:
Request essay removal



