Measuring Concentration of Natural Gas in Air
| ✅ Paper Type: Free Essay | ✅ Subject: Physics |
| ✅ Wordcount: 2624 words | ✅ Published: 12 Mar 2018 |
- Valentin Haemmerli
Measuring concentration of natural gas in air using a catalytic bead sensor and a Wheatstone bridge circuit
Abstract. A vacuum system and a catalytic bead combustible gas sensor were used to calibrate and test an apparatus for measuring the concentration of natural gas in air. Total concentrations ranged between 0%-5% and total pressure from 0.5 bar to 1.5 bar. A Wheatstone bridge circuit was used to measure the output voltage of the sensors and relate this to concentration over the range of pressures. The linear relationship between reaction rate (given by initial rate of change of output voltage) and concentration was most strongly observed at pressures of 1 bar and above. The constant of proportionality for the equation 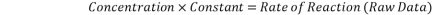 (1) was found to be 8.7 ±0.4 10-4 Vs-1 per % methane for a total system pressure of 1 bar. The relationship broke down for pressures significantly below 1 bar, indicating that the sensors are not reliable in this range.
(1) was found to be 8.7 ±0.4 10-4 Vs-1 per % methane for a total system pressure of 1 bar. The relationship broke down for pressures significantly below 1 bar, indicating that the sensors are not reliable in this range.
- Introduction
Catalytic bead sensors, also known as pellistors [1], are used in a wide range of applications in industry to monitor levels of combustible gases. One such combustible gas is the mixture consisting mainly of methane referred to as natural gas. The catalytic bead sensors can be used to monitor the concentration of natural gas in production facilities, coal mines and industrial processes. This is important because if the concentration of natural gas in air exceeds 5% it becomes explosive [2]. It is especially important to monitor methane concentration because it is usually colourless and odourless [3], making it very difficult to detect without sensors.
An apparatus to measure concentration of natural gas in air can be used to trigger an alarm when there is a concentration greater than the Lower Explosive Limit (LEL), given as a percentage. At this concentration the mixture of gas and air becomes explosive. The apparatus may need to be applied for different pressure environments, not only atmospheric pressure, for example in applications with chemical processes requiring lower or higher pressures. The apparatus has therefore been tested for a range of pressures from 0.5 -1.5 bar.
- Theory
- Sensors
The sensors used are catalytic bead sensors. One sensor is made up of two elements, one sensitive and one non-sensitive. The sensors work by catalysing the oxidation reaction of combustible hydrocarbons in the sensitive element which consists of a platinum wire coated in a compound which facilitates the oxidation reaction and also contains the catalyst for this reaction. The non-sensitive element is identical in most regards, but crucially is missing the oxidizing chemical or has had it poisoned, depending on the specific sensor design used. Poisoning means that the catalyst has been reacted with another chemical to make it inert. The non-sensitive element does not react with combustible gases. The elements are supplied with 3V, and heated up to 400-500ËšC to speed up the reaction. When the oxidation reaction of combustible gases occurs on the sensitive element, the heat of reaction increases the temperature of the element, which changes the resistance in the platinum wire. The non-sensitive element acts as a control for ambient temperature, meaning that in the absence of any combustible gas, the two elements will output exactly the same voltage. This is very useful as it means that change in temperature due to external factors is controlled and the difference in output between the sensitive and non-sensitive elements can be measured using a Wheatstone bridge circuit as described below.
This design means that these sensors detect a multitude of different combustible gases and are therefore not useful for distinguishing between them, meaning they are nonspecific [4]. However, they are very useful for situations where monitoring combustibility is of importance, and they can be applied readily to the task of measuring concentration as they are accurate and have a fast response time. The sensors used are sensitive, with a measurement range of 0-100% of the LEL. This corresponds to 0-5% concentration of methane. One downside of these sensors is that they cannot operate in a vacuum as they rely on combustion, which usually requires at least 15% oxygen [4]. They are also at risk of poisoning since they rely on a coat of catalyst and the presence of certain chemicals can result in a reaction with this catalyst, meaning the sensitive element would no longer facilitate the oxidation reaction and the difference in output between the elements would always be zero.
- Wheatstone Bridge Circuit
Jeong-Yeol Yoon states that “A Wheatstone bridge is an electrical circuit used to measure a very small change in resistance” [5]. A circuit as shown in Figure 1 can be used to measure the output from the sensors, where a small resistance change is expected as a result of the sensitive element heating up due to the presence and reaction of combustible gases. A voltage is supplied at the top and bottom of the diamond of resistors, and the voltage across the middle, between V1 and V2 is measured. The right leg of the bridge should have a large resistance compared to the other leg so that a small change can be detected. The variable resistor allows one to slightly vary the resistance on one leg and so balance the bridge before measurements, zeroing the output.
|
|
|
Figure 1. Diagram of the Wheatstone bridge circuit used to measure output of sensor elements. The typical values supplied by the manufacturer [1] for resistances and input voltage were used. |
- Experimental Method
The first step was to test how sensor output related to concentration for a total pressure of 1bar (atmospheric). Care was taken to ensure that all joints and seals of the vacuum system were tight and that all valves were firmly closed.
The vacuum system used to prepare test mixtures is shown in Figure 2. P1 and P2, the pressure sensors shown in the figure, were used to measure concentration of natural gas and air. P1 had a range of 3 bar, with the zero set to atmospheric pressure (1bar), and vacuum (0bar) set to -1. This was not very precise, with an uncertainty of ±0.1bar and was used to fill up the system with compressed air and the pressure shown by this corresponded to total pressure. P2 was a more precise pressure sensor, ranging from 0 to 50 mbar with uncertainty ±0.5mbar. It was used to carefully add the correct proportion of natural gas to the vacuum, before topping up with compressed air. Using this vacuum system, concentrations ranging from 0-5% natural gas were prepared. Figure 2 also shows the position of the pellistor sensor’s two elements and the connection to the Wheatstone bridge circuit. The output of this circuit was connected to a μV meter which was connected to a computer for data logging. This had a range of -30.00 to 30.00mV with uncertainty ±0.01mV.
|
|
|
|
Figure 2. Vacuum system showing in puts of air and natural gas, outflow of air to vacuum pump, pressure sensors and the sensitive and non-sensitive elements of the sensor built into the system to measure the concentration of natural gas within. |
|
Data logging was carried out for 5 minutes and 30s for concentrations of 1%, 2%, 3%, 4% and 5% at a total pressure of 1 bar. Errors were reduced by zeroing the Wheatstone bridge output using the variable resistor between measurements. This was done to reduce the effect of a natural drift in the output due to very slightly varying conditions in the lab such as temperature and the resistance in the circuit, as well as mechanical vibrations. The bridge circuit supply voltage was kept at a constant 3.00V. Care was taken to leave little time between sealing the system under vacuum and filling with natural gas and air as the seals were not perfect and pressure rose slowly, but noticeably if the system was left at vacuum for an extended period.
This procedure was then repeated for a suitable range of concentrations at total pressures of 0.5, 0.75, 1.25, and 1.5 bar. The same considerations were made for reducing error as above. One thing to note is that at total pressures of less than atmospheric there was always a slight influx of outside air, due to the imperfect seals, however the effect of this was negligible.
- Experimental Results
To find a correlation between the concentration of methane and the bridge output voltage we took the gradient of the initial increasing linear section of the raw data. Figure 3 below shows this for the case with concentration 5% of methane with a total pressure of 1 bar. As can be seen, the measured data falls away as reactant, the natural gas, is used up in the reaction. Figure 3 also shows that there is a very sharp spike as the output voltage varied greatly when the sensor was first switched on. This illustrates that care was needed when selecting which section of the curve to use to calculate the gradient.
|
|
|
Figure 3. Plotting the raw data from the data logging software results in curves such as this. Here the Bridge Output Voltage is plotted versus time for 1 bar total pressure, 5% concentration. Raw data is plotted with the linear trend line (by least squares method) overlaid to show the gradient used. |
This is the right method to use to find concentration because, according to Hammett, “the rate of any chemical reaction is proportional to the product of the concentrations of the substances actually involved in the reaction.” [7] and the gradient of Figure 3 is a rate of reaction. The next step was to establish the gradients, or initial reaction rates, of 1%, 2%, 3%, and 4% methane mixtures. These are shown in Figure 4, along with 5%, for a total pressure of 1 bar. Figure 5 shows these gradients again, but all in order and passing through the origin to better show the steady increase in gradient.
|
|
|
|
|
Figure 4. The linear sections of Figure 3 and the corresponding graphs for the other concentrations at 1 bar are here plotted against time. This shows the differences in gradient. |
Figure 5. Fitted lines of Voltage vs Time for 1 bar for different concentrations, forced through origin for clarity. This shows how much the gradient changed with concentration, the steeper the gradient, the higher the concentration (1%, 2%, 3%, 4%, and 5%). |
Figure 6 shows processed data for 1 bar total pressure. The gradients of the lines from Figures 4 and 5 are plotted against their concentration. This allows us to find a constant linking the raw data to the concentration for this pressure. Table 1 goes on to show the values of this constant for the other pressures analysed. The raw data for these is not shown here, but the process and data is similar to that for 1 bar.
|
|
|
Figure 6. 1 bar concentration relationship, showing rate of change of voltage versus concentration of methane with a linear fit (least squares). The error bars are from the uncertainty in output voltage. |
|
Table 1. Rate of reaction and concentration proportionality constants for range of pressures |
||
|
Constant of Proportionality (10-4 Vs-1 per % methane) |
Standard Error |
|
|
0.75 bar |
6.5 |
±1.6 |
|
1.00 bar |
8.7 |
±0.4 |
|
1.25 bar |
16.2 |
±0.8 |
|
1.50 bar |
25.3 |
±1.9 |
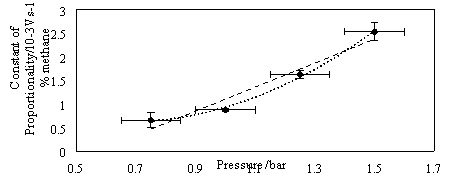
Figure 7 shows the relation between the pressure and the concentration. Also included are a second order polynomial and a linear trend line (fitted by least squares). Vertical error bars are from standard error in Table 1 and horizontal error bars from ±0.1bar uncertainty in total pressure.
|
|
|
Figure 7. Gradient of rate of reaction plotted against concentration, given constant a, versus pressure. |
- Discussion
Figure 6 shows the gradients of the lines in Figures 4 and 5, meaning the rates of reactions at different concentrations, plotted against the concentration of methane. This gives us a relationship between concentration and the initial rate of reaction, the quantity derived from the raw data, for a specific total pressure. For 1 bar this was 8.7±0.4 10-4 Vs-1 per % methane. The error in this comes from a combination of the uncertainty in the pressure measurement leading to uncertainty in concentration corresponding to ±0.1% in the worst case and a small random error in the output voltage of the bridge circuit corresponding to ±2×10-4V.
Figure 7 includes both a polynomial fit and a linear fit. It is unclear if the relationship remains linear or takes some other form at low pressure. The polynomial is almost linear for the three higher pressures, which indicates a strong relationship between pressure and reaction rate for higher pressures. The values and their associated errors in Table 1 come from each plot of initial reaction rate (rate of change of voltage) against concentration for the different pressures. The error is the standard error for these plots.
There was a breakdown of the relationship at low pressures. Data for 0.5 bar total pressure was not included in the results because no clear relationship between output and concentration was found. This indicates that the sensors are not suitable for low pressures, especially when coupled with low concentrations. This resulted in very little output from the sensors, making it difficult to reliably determine an initial reaction rate, which is vital for obtaining a relationship between the raw data and the concentration. The reason for this lack of output was that not enough natural gas particles were interacting with the sensitive element to cause it to heat up and also due to a lower oxygen concentration also slowing down the reaction. This is not a problem in the commercial applications of these types of sensors as they are typically used to detect high concentrations of combustible gases at atmospheric pressure. This does highlight a weakness in the apparatus when used for finding unknown concentrations, however. Another weakness was the inability to measure large pressures precisely, leading to large errors in the total pressure measurements. This has an increased effect on low pressures, which is a further reason for the less reliable data.
- Empirical Relationship
If we give the initial rate of reaction a constant, , and a function of pressure,
, and a function of pressure,  , then
, then
 (2)
(2)
where  is the concentration of methane,
is the concentration of methane, 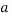 is determined experimentally from the sensor data and
is determined experimentally from the sensor data and  is the polynomial relationship from Figure 7,
is the polynomial relationship from Figure 7,
 (3)
(3)
with the appropriate total pressure, found experimentally from the pressure sensors on the vacuum system, substituted. Using this equation it is possible to use the sensors to determine the concentration of an unknown mixture.
- Conclusions
The aim was to build an apparatus capable of determining the concentration of natural gas in air up to 5%. In order to do this it was necessary to first establish the relationship between sensor output and concentration. This was then repeated at different pressures to understand the effect of a different pressure on the relationship between sensor output and concentration. Finally it was possible to use these relationships to determine the concentration of an unknown mixture of gas and air.
The constant of proportionality for 1 bar pressure was found to be 8.7±0.4 10-4 Vs-1 per % methane. For 0.75 bar it was found to be 6.5±1.6 10-4 Vs-1 per % methane, 1.25 bar was 16.2±0.8 10-4 Vs-1 per % methane, and 1.5 bar was 25.3±1.9 10-4 Vs-1 per % methane. No correlation was found between sensor output and concentration for 0.5 bar.
- Appendix
Division of labour among group members:
- Giuseppe Guarino –main tasks were constructing bridge circuit on protoboard and constructing and soldering strip board circuit which was finally used in data collection
- David Griggs –main tasks were configuring CassyLab software and importing raw data into Microsoft Excel
- Valentin Haemmerli –main tasks were preparing mixtures of natural gas and compressed air in vacuum system and researching sensor operation guidelines
- Shared responsibilities –everyone shared the tasks of checking the circuit, building the vacuum system apparatus and preliminary data analysis.
- References
[1]”Operating Combustible Gas Sensors,” ed: Sixth Sense (sensor manufacturer).
[2]”Material Safety Data Sheet: Methane,” ed: Air Products, 1999.
[3]J. G. Speight, “CHAPTER 1: History and Uses,” in Natural Gas: A Basic Handbook, ed: Euromoney Institutional Investor PLC / Gulf Publishing Company, 2007, pp. 1-33.
[4]L. T. White, “4 – Hazardous Gas Monitoring Sensors,” in Hazardous Gas Monitoring (Fifth Edition), L. T. White, Ed., ed Norwich, NY: William Andrew Publishing, 2001, pp. 81-116.
[5]J.-Y. Yoon, “Wheatstone Bridge,” in Introduction to Biosensors, ed: Springer New York, 2013, pp. 75-86.
[6]”Catalytic Elements – CAT16,” ed: Sixth Sense (sensor manufacturer).
[7]L. P. Hammett, Physical organic chemistry reaction rates, equilibria, and mechanisms. New York; St. Louis; San Francisco [etc.]: McGraw-Hill, 1970.
Cite This Work
To export a reference to this article please select a referencing stye below:
Related Services
View allDMCA / Removal Request
If you are the original writer of this essay and no longer wish to have your work published on UKEssays.com then please click the following link to email our support team:
Request essay removal